The moment of inertia of circle with respect to any axis passing through its centre is given by the following expression. If you were looking for how the value of the ratio pi is calculated or how we know that the same ratio.

Integral Of X X 4 10x 2 26 Math Videos Math Mathematics
Area y dx.

Integral of circle. 3 Contour integrals and Cauchys Theorem 31 Line integrals of complex functions Our goal here will be to discuss integration of complex functions fz u iv with particular regard to analytic functions. Of course one way to think of integration is as antidi erentiation. Its an integral over a closed line eg.
The volume of a sphere can be found similarly by finding the integral of ysqrtr2-x2 rotated about the x-axis. Area of Part of a Circle Given a circle of radius a cut out a tab of height b. See Figure 1 0b a 0 Figure 1.
The circle can be parameterized by zt z0 reit 0 t 2 where r is any positive real number. Using the integral shifting the function as I did and assuming a radius of 2 we end up with an interval 0 15. Using polar coordinates the integral of x n over the unit circle is given by.
Let the circle of radius be centered at the origin. A circle see line integral. The formulas for circumference area and volume of circles and spheres can be explained using integration.
The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral D f xy dA D f x y d A. In the previous section we looked at double integrals over rectangular regions. A line integral of a scalar field is thus a line integral of a vector field where the vectors are always tangential to the line.
Pi is defined to be the ratio of the circumference of a circle over its diameter or 2 times its radius. Section 4-3. The contour integral becomes I C 1 z z0 dz Z2 0 1 zt z0 dzt dt dt Z2 0 ireit reit dt 2i.
Tab cut out of a circle. I frac pi R4 4 where R is the radius of the circle. A natural parameterization of the circular path is given by the angle theta.
Moment of inertia of circle. CIRCLE_INTEGRALS is a FORTRAN90 library which returns the exact value of the integral of any monomial along the circumference of the unit circle in 2D. Sliding the circle in the r direction generates the cone and the integral you are calculating represents calculating the volume of that cone by circular cross sections.
Hence the integrand becomes fairly simple and we choose direct parameterization as our method of integration. N 2 for even n and 0 otherwise using a table of definite integrals or establishing a recurrence relation by parts. Example 1 Evaluate C xy4ds C x y 4 d s where C C is the right half of the circle x2 y2 16 x 2 y 2.
This ratio is a constant since all circles are geometrically similar and linear proportions between any similar geometric figures are constant. But there is also the de nite integral. It is important to note that even though the OP is integrating the left side of the circle the symmetry of the function allows us to integrate either side.
Line integrals of vector fields are independent of the parametrization r in absolute value but they do depend on its orientation. Therefore an integral the gives the area is. d 2 2 n 1.
By adding up the circumferences 2pi r of circles with radius 0 to r integration yields the area pi r2. In particular it is used in complex analysis for contour integralsie closed lines on a complex plane. n r d r d 1 n 2 0 2 cos n.
What is the area of this tab. Lets take a look at an example of a line integral. The circumference of the unit circle in 2D is defined by x2 y2 1 The integrands are all of the form fxy xe1 ye2.
The value of the integral is independent of the radius r. 0 2 0 1 r cos. Basically this is a definition thing.
The equation of the upper semicircle is and the equation of the lower semicircle is. Expressed in terms of the circle diameter D the above equation is equivalent to. Because C is a circle centered at the origin the term sqrt x2 y2 r is a constant along C.
If you slide the circle to a larger distance its radius increases accordingly. One way to compute the area would be split the area into vertical strips and integrate with respect to x. Draw lines between adjacent vertices and between the origin and each vertex.
Double Integrals over General Regions. Where D D is any region. Basically integrating along rather than r Approximate the circle from the inside using a regular n-sided polygon formed from the vertices rcoskn rsinkn where n 2 n and k 0 n 1.

Yea Try Once Please Follow Math Hero Marvelous Post Mathematician Integral Maths Pi Mathematics Mathematical Mat Math Memes Math Humor Math

Contour Integral Of 1 Z With Respect To Z Along The Unit Circle Comple Math Videos Contour The Unit

Find The Area Of The Shaded Region Integral Calculus Example 1 Calculus Region Areas
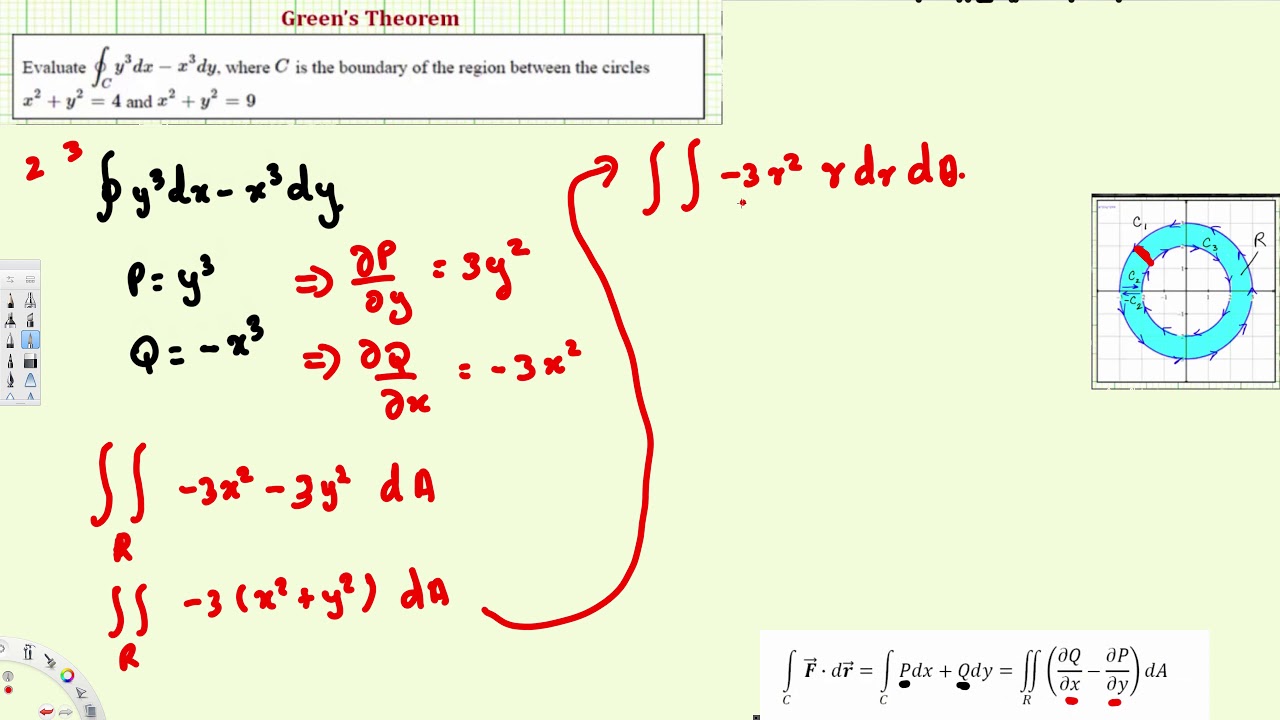
Ex Use Green S Theorem To Evaluate A Line Integral Polar Vector Calculus Vector Calculus Line Integral Calculus

The Integral Of X Arcsin X Trigonometric Substitution Math Videos Calculus Integration By Parts

Revision Exercise For Integration Here Is The Copy Of The Practice Exercises For Integration They Are All Taken Fr Maths Solutions Math Methods Math Formulas

Pauls Online Notes Calculus Ii Integration By Parts Integration By Parts Calculus Online Math

Definite Integrals A Plus Topper Differential Calculus Negative Integers Calculus

How To Integrate Integral With Square Root In Numerator Simplifying Mathematics In Simple Way Integratio How To Memorize Things Solving Equations Mathematics

Compute The Integral Of Sin Sqrt X 3 Using The Integration By Parts An Integration By Parts Problem And Solution Calculus

Pin By Engineer Thileban Explains On Integral Calculus Calculus Expressions Learning

Calculus Integration Differentiation Tricks Maths Shortcuts Matrix Determinants Quadratic Equations Trigonometry Relation Quadratics Mathematics Trigonometry

Geometric Equations Of Circle Mathematics Maths School Collage Formulas Formula Equation Solving Equations Solving Quadratic Equations Studying Math

How To Do U Substitution Easily Explained With 11 Examples Integration By Substitution Math Formulas Substitute

Putnam Definite Integral Hard Problem Evaluate Displaystyle Int 0 Frac Pi 2 Frac Dx 1 Tan X Sqrt 2 Problem Solving Skills Evaluation Mathematics

Rbse Solutions For Class 12 Maths Chapter 11 Application Of Integral Quadrature Ex 11 2 Https Www Rbsesolutions Com Class 12 Maths Math Quotes Studying Math

Basic Integration Formula Sheet Mcq Scholarships Math Formulas Basic Physics Formulas Basic Physics

Rbse Solutions For Class 12 Maths Chapter 11 Application Of Integral Quadrature Miscellaneous Exercise Class 12 Maths Maths Solutions 12th Maths


